1. Overview

The challenge involved a simple PHP-based management board application. The goal was to gain administrative access to retrieve the flag. The core vulnerability was identified as Insecure Direct Object Reference (IDOR) combined with a predictable session ID generation mechanism, which allowed for trivial session impersonation of the administrator user.

2. Initial Code Analysis

The provided source code revealed the application’s logic, primarily within index.php and users.json.

index.php Analysis

The session management functions were the key area of interest:

Function	Description	Vulnerability
generateSessionID($seed)	Generates the session ID as md5($seed).	Predictable: The seed is the user’s index, which is a small, predictable integer.
storeSession($sessionID, $value)	Stores session data in /tmp/$sessionID.	IDOR Potential: Session data is stored in a predictable location based on the predictable ID.
handleLogin()	Authenticates the user and, upon success, sets the session ID.	The $seed passed to generateSessionID is the $idx (index) of the user in the users.json array.

The flag is displayed only if the logged-in user has the moderator attribute set to true:

// index.php (lines 63-65)
<?php if($sessionData->moderator === true) { ?>
<p>Oh, you are moderator! Here you go: <?= file_get_contents("/flag.txt"); ?></p>
<?php } ?>

users.json Analysis

The users.json file provided the list of users and their attributes, including the critical moderator flag.

[
  {
    "username": "test",
    "password": "test",
    "moderator": false
  }, // Index 0
  {
    "username": "alice",
    "password": "WpYcHA1li7@*$Z%mp&W#3ZYIYPw1iVkj",
    "moderator": false
  }, // Index 1
  { 
    "username": "admin",
    "password": "!UCA3P4*Dg@nam4L!oodQK4@TjmC9cnh",
    "moderator": true
  } // Index 2 - TARGET
]

The admin user, who possesses the moderator: true attribute, is located at index 2 in the array.

3. Exploit Strategy

The vulnerability allows us to calculate the session ID for any user, including the administrator, without needing their password.

1. Identify Target Index: The admin user is at index 2.

2. Calculate Admin Session ID: The session ID is md5(index).

   • Admin Session ID = md5("2")
   • md5("2") = c81e728d9d4c2f636f067f89cc14862c

3. Impersonate Session: Set the browser’s sess cookie to the calculated admin session ID.

4. Retrieve Flag: Reload the page, and the application will load the admin’s session data, granting access to the flag.

4. Execution and Flag Retrieval

Step 1: Initial Login (Verification)

A test login with the known credentials (test/test) was performed to observe the session ID generation.

• Login: username=test, password=test
• User Index: 0
• Expected Session ID: md5("0") = cfcd208495d565ef66e7dff9f98764da
• Observed Session ID: cfcd208495d565ef66e7dff9f98764da (Confirmed the mechanism)

Step 2: Session Impersonation

The browser’s sess cookie was manually set to the pre-calculated admin session ID:

document.cookie = "sess=c81e728d9d4c2f636f067f89cc14862c; path=/";
location.reload();

Step 3: Flag Retrieval

Upon page reload, the application recognized the session as belonging to the administrator, and the flag was displayed on the dashboard.

Flag: gctf{1837FA7S_aLwAyS_R4nd0m!z3_Y0uR_C00k!3S!!!_8AJ483H14}

5. Remediation

To fix this vulnerability, the session ID generation must be cryptographically secure and unpredictable.

• Use Secure Session Generation: Replace the predictable md5($idx) with a function that generates a cryptographically secure random string, such as PHP’s session_id() or a custom function using random_bytes() and bin2hex().
• Avoid IDOR: The session data should not be directly linked to a sequential or easily guessable identifier like the user’s array index. The session token should be the only link to the session data, which should be stored securely (e.g., in a database or a secure session store, not in /tmp with a predictable filename).
• Use a Secure Session Handler: Utilize PHP’s built-in session handling mechanisms, which are designed to manage session data securely and prevent such IDOR and session fixation attacks.

---

To the next challenge;

Noisy Neighbour

Challenge Description

The challenge provided an RSA setup with a twist. The public exponent $e$ was intentionally made very large, seemingly to thwart standard Coppersmith attacks on small exponents. The problem statement hints at this:

“I heard Coppersmith attacks small public exponents. I masked mine with a massive random value just to be safe. Bigger is always better, right?”

The provided files were chall.py (the source code) and output.txt (the public parameters and ciphertext). The goal was to recover the 128-bit ticket used as the AES key to decrypt the flag.

Analysis of chall.py

chall.py

import random
from Crypto.Util.number import getPrime, long_to_bytes
from Crypto.Cipher import AES

ticket = random.getrandbits(128)
FLAG = ""
with open('flag.txt', 'r') as flag:
    FLAG = flag.read()

p = getPrime(1024)
q = getPrime(1024)
N = p * q
phi = (p - 1) * (q - 1)

e = getPrime(16) + (random.getrandbits(128) * phi)
enc_ticket = pow(ticket, e, N)

print(f"{N=}")
print(f"{e=}")
print(f"{enc_ticket=}")

cipher = AES.new(long_to_bytes(ticket), AES.MODE_CTR)
nonce = cipher.nonce
enc_flag = cipher.encrypt(FLAG.encode())

print(f"{enc_flag, nonce=}")

output.txt

N=10347242542600406308094534195263088635791365996714020803160250407603636995099715433829129670160192589093770515128152510439089971458386641765448309859819378023880272965050178277879093516918807566027042642100169240017844173793930784667163759562215010481356537422986546632994001754291723194969521748076910835396937977810627980887157551885113202531423733595088875369751631232226097581969479909313254958049277471499732135617616297332871531530596176518111563310557213028740425533103112982126293232786326119238512934754974514742881890899165547139605333761970683944591937361699420431036603767467012489183290578309164784178633
e=3311986667073495779819661492647781665180928338729865042826968893121477288104028672415705332665972755867861711304085148957997662937288947383110908043717598599426017484422084809208910486092822909662298925085867663251659781025068175951771651187222278814345138470007111789992552003468482347964267103806504197977364231330649526292875722283219443425291497285240653190201781346512871589039622122806771109809220085787813190940121150761761463256791250036396820146924876913040030532187290384737376868592733044732294197676117676820815598675412056870600146382869883717018539905436358459822165326225070894181935206514146099686162267119751019096873609300804816456005907
enc_ticket=3946420937017846250393019311609396457338463614723557172414418971956390767261563151514428488890805225021688212721862533753952638354812535035364278722859438604041154655180097577414599710778354857775161040850623041785446044819204867397065653667589062151439260152909905577160138599029484856249429267771263679704326352858922042179435551285375575126876142413991900659195467217772357193174598528534725223102658732326697336473387891654610296170800740197748092566321210843941286260968460061251471684295914144882122101706465054524774059725005866235986370176677629767819073609117398726398647883974883695216900279944685266429904
enc_flag, nonce=(b'`\x8d\x9e\x1e\xd4!\xf5\xe3\xf8,\xfb\x16UV\xcc\xae\xe6G\x91F\x06\x157)\x99|;\xb0\xf5\x87\xa2R\xa8\xd4H\xd16\xa6\xd6\xd1r\xe7 C\xd6i\x83\xb9\xf9\xf7f=\xab\x16', b'\xf1\xdbF)\x91\xc5\xb4$')

The source code reveals the construction of the RSA parameters:

1. Modulus $N$: $N = p \cdot q$, where $p$ and $q$ are 1024-bit primes, making $N$ a 2048-bit modulus.
2. Euler’s Totient $\phi(N)$: $\phi = (p-1)(q-1)$.
3. Public Exponent $e$: $$e = \text{getPrime}(16) + (\text{random.getrandbits}(128) \cdot \phi)$$ This is the core vulnerability. The exponent $e$ is constructed as: $$e = e*{\text{small}} + R \cdot \phi$$ where $e*{\text{small}}$ is a small 16-bit prime, and $R$ is a 128-bit random integer.
4. Encryption: The 128-bit ticket is encrypted using standard RSA: $$\text{enc_ticket} = \text{ticket}^e \pmod{N}$$
5. Flag Encryption: The ticket is used as the AES key (after converting to bytes) to encrypt the flag using AES in CTR mode.

Cryptographic Vulnerability: Noisy RSA

The construction of $e$ is a classic example of Noisy RSA or a variation of the Coppersmith attack on small $\phi(N)$ error.

The relationship between $N$ and $\phi$ is: $$\phi = N - (p+q) + 1$$ Since $p$ and $q$ are 1024-bit primes, $p+q$ is approximately $2 \cdot 2^{1023} \approx 2^{1024}$, which is a value much smaller than $N$ (2048 bits). This means $\phi$ is very close to $N$.

Substituting $\phi$ into the equation for $e$: $$e = e*{\text{small}} + R \cdot (N - (p+q) + 1)$$ $$e = R \cdot N + (e*{\text{small}} + R - R \cdot (p+q))$$

Let $K = e - R \cdot N$. Since $e$ and $N$ are known, and $R$ is a small integer, $K$ is a known value. $$K = e_{\text{small}} + R - R \cdot (p+q)$$

The values are:

• $N \approx 2^{2048}$
• $e \approx 2^{2048}$
• $R \approx 2^{128}$ (but since $e$ and $N$ are the same bit length, $R$ must be a very small integer, as $e$ is only slightly larger than $R \cdot \phi \approx R \cdot N$).
• $e_{\text{small}} < 2^{16}$
• $p+q \approx 2^{1024}$

The key insight is that $R$ must be a small integer. We can approximate $R$ by calculating the integer division of $e$ by $N$: $$R \approx \lfloor e / N \rfloor$$

From the provided output.txt:

• $N \approx 1.0347 \times 10^{616}$
• $e \approx 3.3119 \times 10^{616}$
• $R_{\text{approx}} = \lfloor e / N \rfloor = 3$

With $R=3$, we can rearrange the equation for $K$ to solve for $S = p+q$: $$R \cdot (p+q) = e*{\text{small}} + R - K$$ $$p+q = S = \frac{e*{\text{small}} + R - K}{R}$$

Since $S$ must be an integer, $e*{\text{small}} + R - K$ must be divisible by $R$. We can iterate over all possible small prime values for $e*{\text{small}}$ (up to $2^{16}$) and check this divisibility condition.

Factoring $N$ and Decryption

Once we find the correct $e_{\text{small}}$ and thus $S = p+q$, we can factor $N$ using the property that $p$ and $q$ are the roots of the quadratic equation: $$x^2 - S \cdot x + N = 0$$

The roots are given by the quadratic formula: $$p, q = \frac{S \pm \sqrt{S^2 - 4N}}{2}$$

The steps to solve the challenge are:

1. Determine $R$: Calculate $R_{\text{approx}} = \lfloor e / N \rfloor$. We found $R=3$.
2. Iterate for $e_{\text{small}}$: Iterate through all primes $e_{\text{small}} \in [2, 2^{16}]$.
3. Check Divisibility: For each $e*{\text{small}}$, check if $(e*{\text{small}} + R - K)$ is divisible by $R$.
4. Calculate $S$: If divisible, calculate $S = p+q$.
5. Check Discriminant: Check if the discriminant $\Delta = S^2 - 4N$ is a perfect square.
6. Factor $N$: If $\Delta$ is a perfect square, calculate $p$ and $q$.
7. Decrypt: Calculate $\phi = (p-1)(q-1)$, the private exponent $d = e^{-1} \pmod{\phi}$, and the ticket by decrypting $\text{enc_ticket}$.
8. Recover Flag: Use the ticket as the AES key to decrypt the flag ciphertext.

The Python solver script implemented this logic:

# ... (imports and public parameters)

def solve():
    # R is the integer part of e / N.
    R_approx = e // N
    R_candidates = [R_approx - 1, R_approx, R_approx + 1]
    
    for R in R_candidates:
        K = e - R * N
        
        for e_small_candidate in range(2, 2**16):
            if is_prime(e_small_candidate):
                if (e_small_candidate - K) % R == 0:
                    S = 1 + (e_small_candidate - K) // R
                    
                    Delta = S**2 - 4 * N
                    
                    if Delta > 0 and is_square(Delta):
                        sqrt_Delta = math.isqrt(Delta)
                        p = (S + sqrt_Delta) // 2
                        q = (S - sqrt_Delta) // 2
                        
                        if p * q == N:
                            # Found the factors!
                            phi = (p - 1) * (q - 1)
                            d = inverse(e, phi)
                            ticket = pow(enc_ticket, d, N)
                            
                            # Decrypt the flag
                            key = long_to_bytes(ticket)
                            cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
                            dec_flag = cipher.decrypt(enc_flag)
                            
                            return dec_flag.decode()
    
    return "Attack failed."

Flag

Executing the solver script successfully recovered the flag:

gctf{c0pp3rsm17h_ste4ling_y0ur_sm4ll_r00ts_2025-2079}

THE NEXT CHALLENGE;

gitresethard

Overview

The challenge simulates a scenario where a developer (“Kevin”) nukes a repository using:

git reset —hard

git push —force

The working tree is gone, the commits are “lost,” and you’re given only a compressed disk image containing a bare .git directory.

Your job is to recover the “lost” commit, extract the malicious file hidden inside it, and decrypt the final flag.

The challenge is about understanding:

Git object storage

Dangling commits

Using git fsck to recover unreachable data

Extracting file versions directly from Git objects

Basic AES decryption

Step 1 — Understanding the Provided Files

After unpacking the challenge bundle, you end up with:

repo/ # This is actually the .git directory

repo.tar.gz # Archive containing the same repo directory

Important: repo/ is not a full project. It is the .git folder itself.

There is no working tree, and Git will not operate normally unless you specify one.

Step 2 — Creating a Work-Tree

Git requires a working directory even if all you have is .git.

So you create one:

mkdir -p ~/Downloads/ctf/glacier/work

Step 3 — Running git fsck to Recover Lost Commits

Because the repo was hard-reset and force-pushed, the commit you want is now unreachable.

We point Git to the correct locations:

GITDIR=$HOME/Downloads/ctf/glacier/gitresethard/repo

WORK=$HOME/Downloads/ctf/glacier/work

Then run:

git —git-dir=“$GITDIR” —work-tree=“$WORK” fsck —no-reflogs —lost-found

Git scans all objects in the object database and prints out anything that’s valid but not referenced.

You get:

dangling commit 6a81c76ebba614823433d7caf0ea7e523a998fcb

This unreachable commit is the challenge’s core.

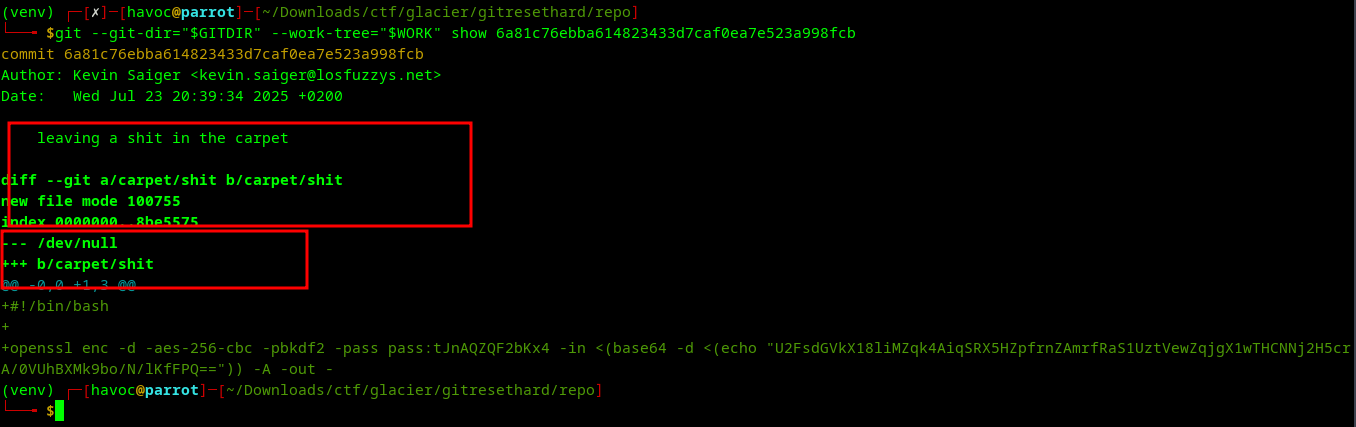
Step 4 — Inspecting the Dangling Commit

Show it:

git —git-dir=“$GITDIR” —work-tree=“$WORK” show 6a81c76eb…

You see that the commit modifies:

carpet/shit

This is the file you need to extract.

Step 5 — Extracting the File From the Commit

Directly pull the blob from the Git object:

git —git-dir=“$GITDIR” —work-tree=“$WORK” \

\ show 6a81c76eb…:carpet/shit \

> “$WORK/shit.sh”

When you view the file:

cat $WORK/shit.sh

you find:

A large base64-encoded blob

An AES-256-CBC decrypt command

A passphrase hardcoded inside the script

Example (simplified):

echo “U2FsdGVkX1…” | base64 -d | openssl enc -d -aes-256-cbc -pbkdf2 -pass pass:tJnAQZQF2bKx4

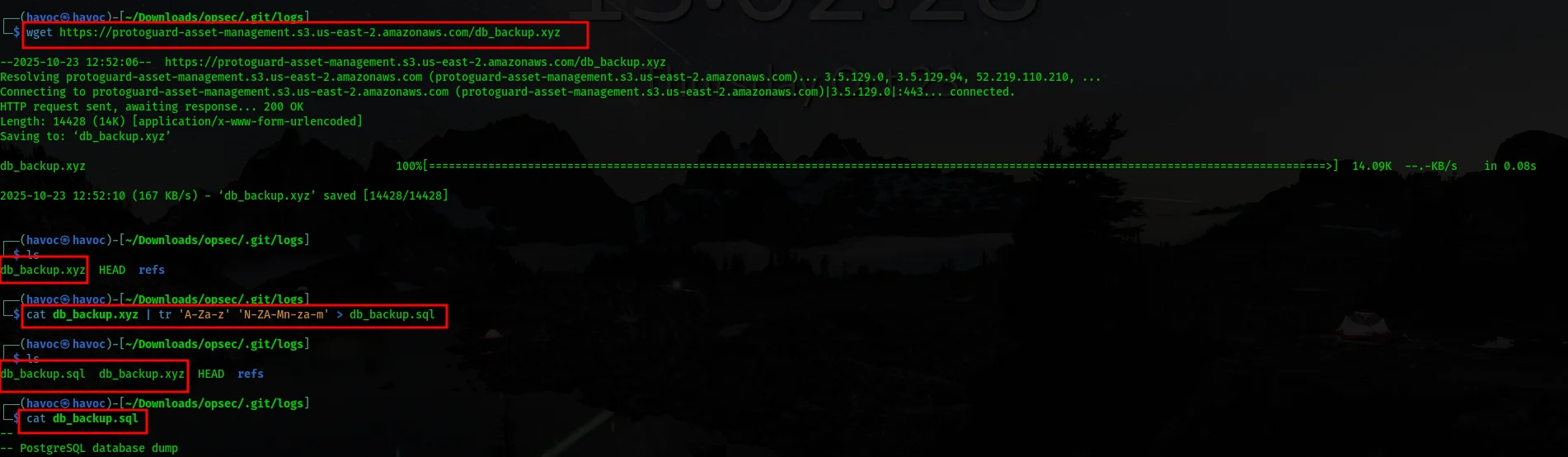
Step 6 — Decrypting the Embedded Payload

Copy the base64 payload and the password, then run:

echo "" | base64 -d \

| openssl enc -d -aes-256-cbc -pbkdf2 -pass pass:

This reveals the final flag.In this challenge:

gctf{0113_wh0_g1t_r3s3t3d_th3_c4t_4789}

Lessons Learned

1. Git reset + force push doesn’t erase history

If you have the .git directory, you can recover far more than people think.

2. The working tree is irrelevant

Git’s real data lives in:

3. fsck is your best friend for forensics

It lists unreachable:

• commits
• blobs
• trees

4. Git is a forensic goldmine

Unless objects have been GC’d (git gc), recovery is trivial.

Final Thoughts

This challenge was straight-forward but exposes a huge blind spot developers have:

***They think Git “deletes” things. It doesn’t.

It leaves a trail for anyone competent to follow.***

The next challenge;

1. Overview

This was the introductory reversing challenge.

The binary didn’t hide behind obfuscation, packing, or VM tricks — it simply embedded the flag in a lightly transformed way.

The goal:

Figure out how the program validates input and extract the flag logic directly. here we go buddies;

2. Initial Recon

Running file on the binary showed it was a standard ELF:

ELF 64-bit LSB executable, x86-64

Running strings immediately exposed suspicious fragments: but nothing important

so we go to binaryninja and dissasemple the binary

to the main we got this

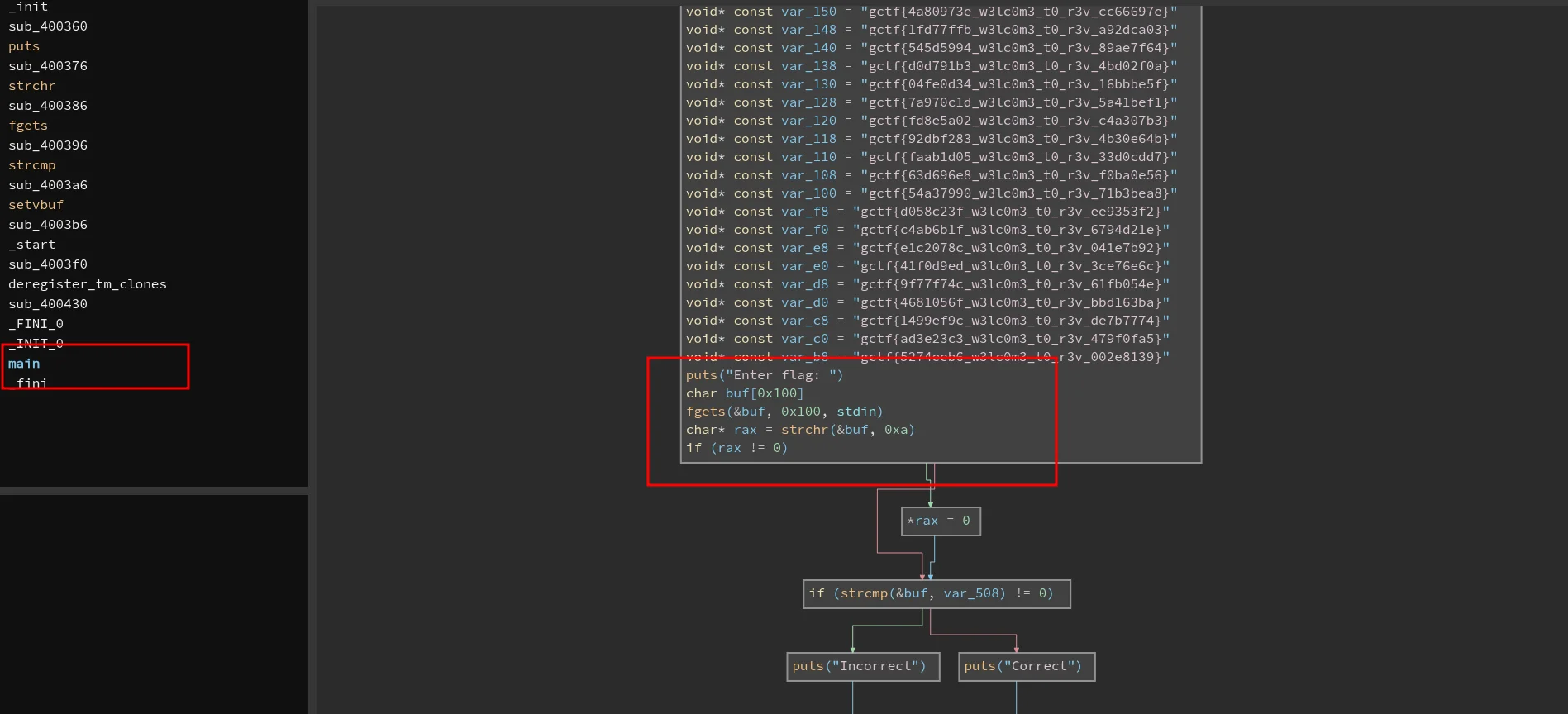
by keeping in mind what main gave us we are in the clear. on the

char*var_508

we got it

the flag is

gctf{bd88c4d4_w3lc0m3_t0_r3v_574dc8aa}

so year we got this easy peasy

---

happy hacking!!!!